Estudian cómo prevenir la dispersión de enfermedades
Un equipo de investigadores del Grupo de Estudios Básicos e Interdisciplinarios (GEBI) de Exactas elaboró un modelo matemático original para analizar los efectos de diferentes medidas de prevención y combate de una epidemia. El trabajo fue publicado en la revista científica Physical Review E.
En 1871, los habitantes de la ciudad de Buenos Aires padecieron una epidemia de fiebre amarilla que ocasionó la muerte de alrededor del 8% de los porteños.
Los decesos habrían sido muchísimos menos si las autoridades sanitarias de la época no hubieran creído que la peste estaba relacionada con las aglomeraciones humanas. Porque esta falsa idea llevó a desalojar conventillos y a promover evacuaciones que diseminaron la enfermedad y empeoraron la situación.
“Hicimos una simulación de cómo evolucionó el foco inicial de aquella epidemia y, comparando con documentos de la época, nuestro modelo matemático reproduce fielmente la distribución espacial de la enfermedad y su mortalidad diaria a lo largo del tiempo”, comenta el doctor Hernán Solari, investigador del Conicet en el Grupo de Estudios Básicos e Interdisciplinarios (GEBI) de la Facultad de Ciencias Exactas y Naturales de la UBA. “Pero hay un segundo momento, cuando se disemina la epidemia, que nuestro modelo no pudo prever”, completa.
Lo que las autoridades sanitarias de aquel entonces no podían saber y el modelo matemático de Solari no podía prever era el efecto de la movilidad humana sobre lo que se denomina “fuerza de la epidemia”, un parámetro que refleja la cantidad de gente que se infecta diariamente durante un evento epidémico.
Ahora, un artículo publicado en la revista científica Physical Review E da cuenta de un modelo que incluye los desplazamientos humanos en sus ecuaciones y que es útil para simular una epidemia de fiebre amarilla o de dengue. “Nuestro modelo confirma que el movimiento de la gente es crucial en la propagación de estas enfermedades y permite explorar con cierto realismo políticas de prevención y combate”, señala el doctor Claudio Dorso, investigador del Conicet en el GEBI, quien firma el trabajo junto con Marcelo Otero, Daniel Barmak y el propio Solari.
Modelo integral
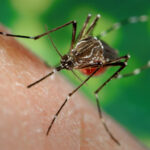
En 1871 no se sabía que el responsable de la fiebre amarilla es un virus transmitido por la picadura del mosquito Aedes aegypti, insecto que también transmite el virus del dengue. Tampoco se sabía que el mosquito adquiere esos virus al picar a una persona infectada. En otras palabras, el hombre es un reservorio del virus y lo traslada de un lado a otro mucho más rápido que el mosquito.
Hasta ahora, los modelos que trataban de simular la diseminación de las enfermedades transmitidas por el Aedes aegypti sólo tomaban en cuenta la dinámica del mosquito. De hecho, un trabajo previo de estos investigadores logró predecir con mucha precisión las fechas de aparición y desaparición del insecto en la ciudad de Buenos Aires, así como el momento de máxima abundancia del mosquito. Pero ese modelo no permitía pronosticar cómo se propagaría una eventual epidemia.
Con datos de las redes de telefonía celular, que registran el desplazamiento de la gente mientras va pasando por distintas antenas, en Estados Unidos habían estudiado las particularidades del movimiento de las personas. “A partir de esos resultados, pudimos crear un modelo que describe la movilidad de las personas y, luego, integrarlo al modelo para mosquitos”, explica Dorso.
Transformar en ecuaciones la complejidad del comportamiento humano no es tarea fácil. Sin embargo, Dorso relativiza: “Si uno hace un análisis estadístico, el movimiento que hacen los humanos es altamente repetitivo y, por lo tanto, bastante predecible”.
En el mundo, existen modelos que analizan el efecto de la movilidad humana en la transmisión de patologías infecciosas que se transmiten de persona a persona, como la gripe: “Este es el primer modelo de enfermedades transmitidas por vectores que integra la conducta humana en sus ecuaciones”, apuntan.
Según los investigadores, el nuevo modelo permite comprender la evolución de la epidemia de fiebre amarilla de 1871 y la circulación de dengue en Buenos Aires durante la epidemia de 2009.
“Una virtud del modelo es que es altamente eficiente, lo cual no solo posibilita utilizarlo en una computadora personal sino, también, usarlo en mayor escala y abarcar poblaciones de millones de personas”, destaca Solari.
Mientras intentan infructuosamente conseguir datos de todo el país acerca de cómo evolucionó la última epidemia de dengue –“son imprescindibles para perfeccionar el modelo”, explican-, los investigadores se dedican a simular los efectos de diversas medidas de profilaxis y de prevención en diferentes momentos y condiciones de una epidemia.
“Planteando diferentes escenarios buscamos responder infinidad de preguntas. Por ejemplo, cuál es el momento y lugar para realizar una fumigación, o si la gente debería quedarse en su casa durante un determinado lapso de tiempo, o si es útil aislar a los enfermos”, ilustra Dorso.
Juegan con la computadora. Pero no es para sumar puntos en el Tetris, sino para analizar las mejores alternativas sanitarias para enfrentar la próxima epidemia.